Contact
Fleurianne Bertrand
TU Chemnitz
Fakultät für Mathematik
Reichenhainer Straße 41
09126 Chemnitz
Germany
TU Chemnitz
Numerical analysis and Optimisation
with Prof. Daniele Boffi, founded by KAUST.
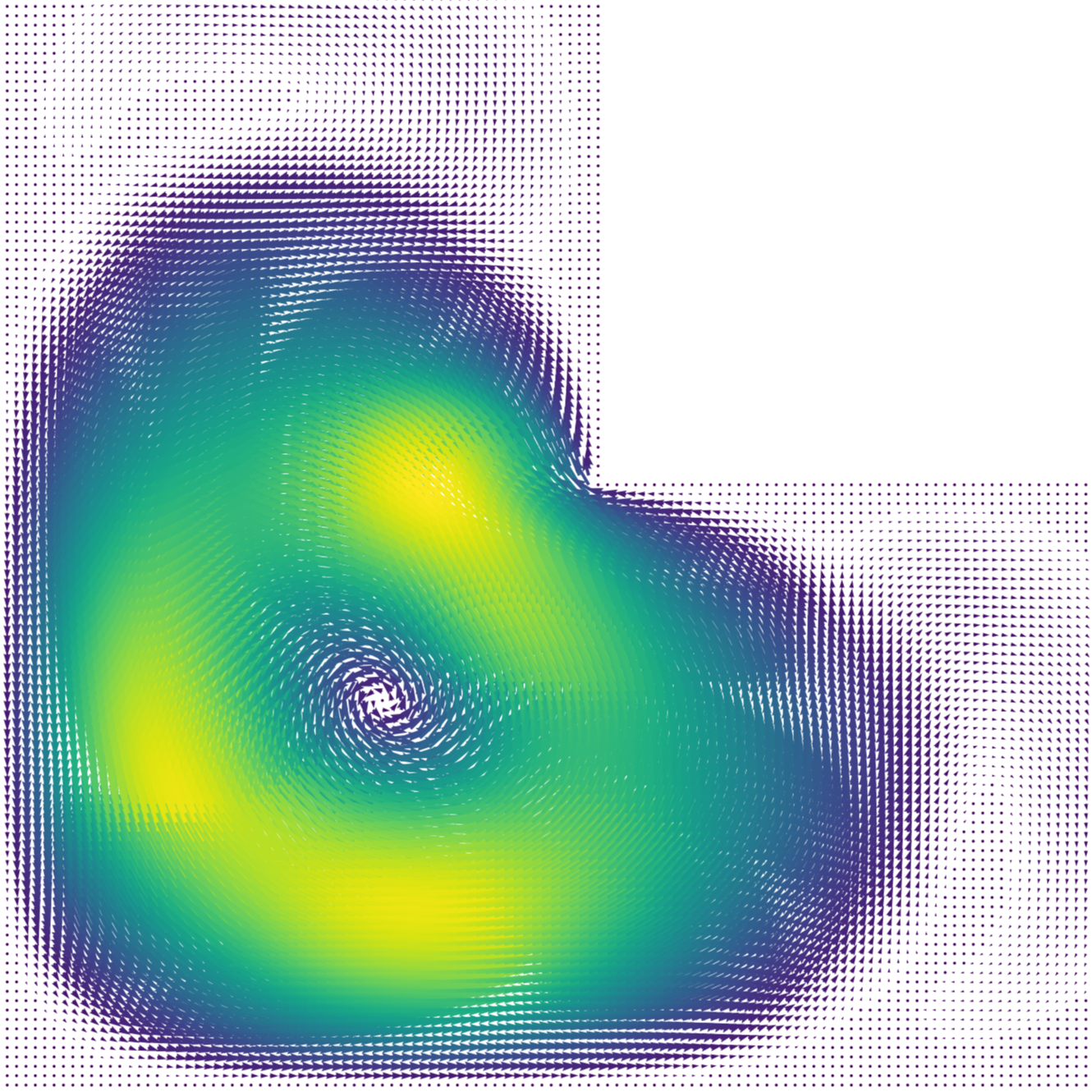
We aim at reducing the complexity of the simulations of large, complex systems described in terms of partial differential equations in the spirit of Reduced Order Methods (ROMs).
As a first step, we considered a reduced order method for the approximation of the eigensolutions of the Laplace problem with Dirichlet boundary condition, see our recent preprint here.
with Prof. Caroline Birk and Prof. Christian Meyer, founded by
Mercator Research Center Ruhr (MERCUR).
Rapid temperature changes may induce thermal stresses, which lead to the initiation and acceleration of damage and fracture processes in structures. The aim of this project is to develop efficient simulation methods for the prediction of thermally-induced crack propagation processes. To this end, a global model based on the scaled boundary finite element method is coupled with a local thermoelastic two-field damage model. Another aim of this project is to develop appropriate error estimators in order to reduce the number of degrees of freedom.
See also our recent publication on the convergence rate of the SBFEM.

with Prof. Jörg Schröder and Prof. Gerhard Starke, founded in the DFG priority programm SPP 1748.
The main objective of this Priority Programme is the development of modern non-conventional discretisation methods, including the mathematical analysis for geometrically as well as physically non-linear problems in the fields of e.g. incompressibility, anisotropies and discontinuities (cracks, contact).
founded by Universität Duisburg-Essen, programm for excellent young researcher.
A common way to determine the displacement of a structure under forces, the so-called primal approach, is based on the minimisation of an energy depending on the displacement variable. However, this so-called primal approach does not lead to uniform accuracy for nearly incompressible materials such as common blood vessel walls or the heart muscle, except if the degree of the polynomial approximation is kept very high, leading to a high computational effort.
In solid mechanics, the quantity expressing the internal forces is the stress. Surely, the stresses can be computed from the primal approach in a post-processing but this approach leads to stresses, which divergence is not squarely integrable. In other words, they are not H(div)-conforming and surface or interface traction forces cannot be evaluated. Moreover, momentum cannot be exactly conserved. As this quantities are driving quantities the standard methods are not accurate enough in many challenging applications and stress-based method are known to be a game changer to obtain guaranteed accuracy. However, in solid mechanics, the symmetric gradient arising in the corresponding partial differential equation is not an easy condition to impose at the discrete level. The conforming discretisation of those stresses, the so-called Arnold-Winter approach, is highly sophisticated and increase the computational cost enormously.
To address the aforementioned issue, my overall aim is to develop numerical methods with very high and guaranteed accuracy. The key objectives are:
• Guaranteed accuracy: given a tolerance, the true error is less and greater than the tolerance, up to multiplicative constants.
• Robustness: the constants in the error bounds don’t depend on model parameter.
• Accessibility : the computational cost is moderate. The constants in the error bounds depend only on local quantities (i.e. mesh-size, shape of the element) and not on global quantities (such that as Poincaré constant of the whole domain)

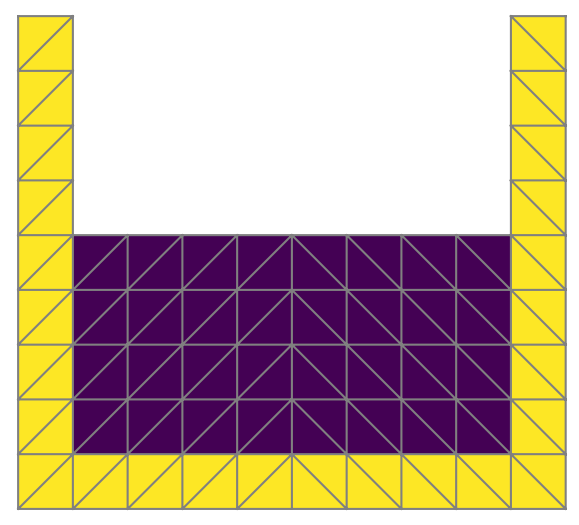
Elliptic boundary value problems arising in science and engineering are often posed on domains with curved boundaries. For low-order finite elements it is usually sufficient to use a polygonal approximation of the boundary in order to ensure that the finite element order of convergence is not affected by the inaccurate representation of the boundary. For higher-order finite elements a more accurate representation of the boundary is required which is usually achieved by isoparametric finite elements; i.e., the same finite element space is used once more for the parametrization of a more accurate domain approximation.
Finite element methods which simultaneously approximate scalar (potential) and vector (flux) unknowns are also widely used due to the fact that improved approximation of fluxes is sometimes a desirable goal. Favorable conservation properties or inherent error control are among the advantages of these methods. The treatment of curved boundaries in the context of edge- or face-based finite elements where Neumann boundary conditions are imposed on the normal flux is, however, rather seldom mentioned in the literature. A thorough analysis of the effect of polygonal boundary approximation on the Raviart–Thomas finite element approximations seemed to be missing and was the purpose of this project.
Related publications:
Parametric Raviart-Thomas elements for mixed methods on domains with curved surfaces
Bertrand, F. & Starke, G., 2016, In: SIAM Journal on Numerical Analysis. 54, 6, p. 3648-3667 20
First-order system least squares on curved boundaries: Lowest-order Raviart-Thomas elements
Bertrand, F., Münzenmaier, S. & Starke, G., 2014, In: SIAM Journal on Numerical Analysis. 52, 2, p. 880-894
First-order system least squares on curved boundaries: Higher-order Raviart-Thomas elements
Bertrand, F., Münzenmaier, S. & Starke, G., 2014, In: SIAM Journal on Numerical Analysis. 52, 6, p. 3165-3180 16 p.
First-order system least-squares for interface problems
Bertrand, F., 2018, In: SIAM Journal on Numerical Analysis. 56, 3, p. 1711-1730 20 p.